Міщук Юлія Констянтинівна
Факультет:
Комп'ютерных наук і технологій
Спеціальність:
Програмне забезпечення автоматизованих систем
Тема магістерської диссертації:
Аналіз ефективності обчислювальних систем з використанням марковської моделі
Керівник:
Фельдман Лев Петрович
Автореферат за темою магістерської роботи:
«Аналіз ефективності обчислювальних систем з використанням марковської моделі»
Цілі і завдання
- Огляд і аналіз сучасних обчислювальних систем.
- Огляд і аналіз методів аналізу обчислювальних систем.
- Розробити модель однорідного кластера зі спільним використанням дискового простору
- Програмно реалізувати модель на паралельних системах.
- Оцінити ефективність реалізації.
Актуальність
У зв'язку з необхідністю збільшення обчислюваних потужностей у багатьох сферах життєдіяльності людини, активно розробляються алгоритми поліпшення роботи обчислювальних систем — систем обробки даних, налаштованих на вирішення завдань, конкретної галузі застосування. Основоположними в теорії обчислювальних систем є моделі і апарат теорії марковських процесів.
Поняття архітектури високопродуктивної системи є досить широким, оскільки під архітектурою можна розуміти і спосіб паралельної обробки даних, який використовується в системі, і організацію пам'яті, і топологію зв'язку між процесорами, і спосіб виконання системою арифметичних операцій. Розглядається кластерна архітектура багатопроцесорних обчислювальних систем [1]. З огляду на трудомісткість і великі обсяги даних, марковські моделі не використовувалися у великих системах, тому проблема є актуальною [2]. У даній роботі необхідно проаналізувати ефективність розпаралелювання методу і з'ясувати, наскільки прискорилося моделювання багатопроцесорної системи [3].
Наукова значимість
Створення і використання сучасних суперкомп'ютерних систем стало в наш час одним з основних напрямків у провідних країнах світу. Однією з основних проблем, що виникають при проектуванні та експлуатації паралельних і розподілених обчислювальних систем є вироблення рекомендацій раціонального використання ресурсів обчислювального середовища. Одним з ефективних способів вирішення цієї проблеми може бути використання рзультатов безперервних або дискретних аналітичних моделей [4].
Огляд досліджень і розробок по темі
Існує цілий ряд галузей (таких, як: науки про Землю (фізика атмосфери, метеорологія, кліматологія, фізика океану); математична лінгвістика (розпізнавання мови, аналіз тексту); біологія, екологія; економіка; соціальні науки; інформатика (розподілені обчислювальні системи, розпізнавання образів, ведення БД); медицина; фармацевтика і т.д.), у яких виникає необхідність вирішення великих обсягів обчислень за прийнятний лічильний час [5].
Зростання обчислювальної потужності комп'ютерних систем, поява сучасних суперкомп'ютерів, кластерів робочих станцій, постійне підвищення потужності комп'ютерних систем призводить до того, що завдання, які ще в недалекому минулому не могли бути вирішені в реальному масштабі часу, успішно вирішуються завдяки використанню паралельних алгоритмів, реалізується на багатопроцесорних системах, що володіють високою швидкодією.
У зв'язку з цим, активно розробляються алгоритми поліпшення роботи обчислювальних систем. Роботи в цьому напрямку не втрачають своєї актуальності і вимагають подальшого розвитку, знаходження нових рішень.
В ДонНТУ над цими питаннями працюють:
- Доктор технічних наук, професор, Фельдман Лев Петрович,
- Кандидат технічних наук, доцент Михайлова Тетяна Василівна,
- Кандидат технічних наук, доцент Ладиженський Юрій Валентинович
так само в останні роки подібної тематикою займалися магістранти:
Дяченко Тетяна Федорівна (Керівник: к.физ-мат.н., доцент Дацун Наталія Миколаївна)
Тема магістерської роботи: «Дослідження паралельного алгоритму побудови Марковських моделей обчислювальних систем»Кучереносова Ольга Володимирівна (Керівник: д.т.н., професор Башков Євген Олександрович)
Тема магістерської роботи: «Дослідження ефективності паралельних обчислювальних систем»Алтинпара Євген Олегович (Керівник: к.т.н., доцент Ладиженський Юрій Валентинович)
Тема магістерської роботи: «Рішення задач великої розмірності на кластері»Морозов Роман Миколайович (Керівник: к.т.н., доцент Ладиженський Юрій Валентинович)
Тема магістерської роботи: «Розподілені алгоритми розв'язання задач високої розмірності на обчислювальному кластері»Завалкін Дмитро Олександрович (Керівник: д.т.н., професор Фельдман Лев Петрович)
Тема магістерської роботи: «Аналіз та оцінка ефективності паралельних різницевих методів рішення ОДУ на кластері»Аль-Масрі Мохаммед Ріда (Керівник: к.т.н., доцент Ладиженський Юрій Валентинович)
Тема магістерської роботи: «Паралельні методи розв'язання систем лінійних алгебраїчних рівнянь на обчислювальному кластері»
Общие понятия
Структура ОС — це сукупність комплексіруемих елементів та їх зв'язків. В якості елементів ОС виступають окремі ЕОМ і процесори.
Існує велика кількість ознак, за якими класифікують обчислювальні системи: за цільовим призначенням та виконуваних функцій, за типами і кількістю ЕОМ або процесорів, з архітектури системи.
В 1966 році Майклом Флінном (Flynn) був запропонований надзвичайно зручний підхід до класифікації архітектур обчислювальних систем [6]. В основу було покладено поняття потоку, під яким розуміється послідовність елементів, команд або даних, оброблювана процесором. Відповідна система класифікації заснована на розгляді числа потоків інструкцій і потоків даних і описує чотири архітектурні класу:
-
SISD = Single Instruction Single Data
Одиночний потік команд і одиночний потік даних. До цього класу належать послідовні комп'ютерні системи, які мають один центральний процесор, здатний обробляти тільки один потік послідовно виконуваних інструкцій.
-
MISD = Multiple Instruction Single Data
Множинний потік команд і одиночний потік даних. Теоретично в цьому типі машин безліч інструкцій повинно виконуватися над єдиним потоком даних. До цих пір ні однієї реальної машини, що потрапляє в даний клас, не було створено.
-
SIMD = Single Instruction Multiple Data
Одиночний потік команд і множинний потік даних. Ці системи зазвичай мають велику кількість процесорів, в межах від 1024 до 16384, які можуть виконувати одну і ту ж інструкцію щодо різних даних у жорсткій конфігурації. Єдина інструкція паралельно виконується над багатьма елементами даних.
-
MIMD = Multiple Instruction Multiple Data
Множинний потік команд і множинний потік даних. Ці машини паралельно виконують кілька потоків інструкцій над різними потоками даних. На відміну від багатопроцесорних SISD-машин, згаданих вище, команди і дані пов'язані, тому що вони представляють різні частини однієї і тієї ж виконуваного завдання. Наприклад, MIMD-системи можуть паралельно виконувати безліч підзадач, з метою скорочення часу виконання основного завдання.
Слід зазначити, що хоча систематика Флінна широко використовується при конкретизації типів комп'ютерних систем, така класифікація призводить до того, що практично всі види паралельних систем (незважаючи на їх суттєву різнорідність) належать до однієї групи MIMD. Як результат, багатьма дослідниками робилися неодноразові спроби деталізації систематики Флінна. Так, наприклад, для класу MIMD запропонована практично загальновизнана структурну схему, в якій подальший поділ типів багатопроцесорних систем грунтується на використовуваних способи організації оперативної пам'яті в цих системах [7].
Кластер представляє собою два або більше комп'ютерів (часто званих вузлами), що об'єднуються за допомогою мережевих технологій на базі шинної архітектури або комутатора і постають перед користувачами в якості єдиного інформаційно-обчислювального ресурсу. В якості вузлів кластера можуть бути обрані сервери, робочі станції і навіть звичайні персональні комп'ютери. Перевага кластеризації для підвищення працездатності стає очевидним у разі збою будь-якого вузла: при цьому другий вузол кластеру може взяти на себе навантаження несправного вузла, і користувачі не помітять переривання в доступі.
Кластеризація може бути здійснена на різних рівнях комп'ютерної системи, включаючи апаратне забезпечення, операційні системи, програми-утиліти, системи управління та програми. Чим більше рівнів системи об'єднані кластерної технологією, тим вище надійність, масштабованість та керованість кластеру.
Модель однорідного кластера зі спільним використанням дискового простору
Однією з систем класифікації кластерних систем є класифікація по спільному використанню одних і тих же дисків окремими вузлами: кластери з спільним і роздільним використанням дискового простору [8].
У роботі розглянуто модель кластеру зі спільним використанням дискового простору.
Реалізація
Визначальними при розпаралелюванні алгоритму є:
- кількість вузлів обчислювального кластеру;
- кількість процесів на кластері;
- спосіб розміщення даних;
- методи комутації.
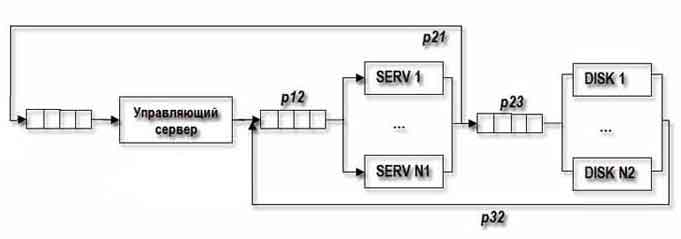
Рисунок 1 — Структурна схема кластеру зі спільним використанням дискового простору.
У обчислювальній системі, наведеною на рисунку 1, М завдань або користувачів, N1 однотипних кластерів-серверів і N2 дисків, на яких зберігаються дані. Кожен з М користувачів посилає з імовірністю P 12, запит до одного з N1 серверів, які, у свою чергу, обробляючи цей запит, звертаються до одного з N2 дисків з імовірністю P 23. Ймовірність завершення обслуговування завдання одним з N2 дисків і надходження на i-й сервер тоді буде - P 32 [i = 1 .. N1].
Алгоритм
Алгоритм, застосований у паралельній реалізації марковських моделей [2,10], складається з двох частин: обчислень матриці перехідних ймовірностей і вектора стаціонарних ймовірностей.
Розрахунок стаціонарних ймовірностей реалізований з використанням ітераційного алгоритму, в якому в якості базового використовується алгоритм множення матриці на вектор.
Обчислення елемента матриці перехідних ймовірностей не залежить від сусідніх елементів, отже, в основі паралельної реалізації цієї частини паралельного алгоритму можна використовувати принцип розпаралелювання за даними [4]. Суть полягає в тому, в задачі виділені окремі незалежні частини — гілки програми, які за наявності декількох оброблювальних пристроїв можуть виконуватися паралельно і незалежно один від одного.
У якості базової підзадачі в алгоритмі взято розрахунок рядка матриці перехідних ймовірностей, яка характеризується однаковою обчислювальної трудомісткістю.
Оцінка ефективності
Обчислення основних характеристик відбувається за такими формулами:
 |
Середнє число вільних пристроїв у s-му вузлі обчислюється за формулою. |
 |
Середнє число зайнятих пристроїв у s-му вузлі визначається за формулою. |
 |
Завантаження пристроїв визначається за наступною формулою. |
 |
Середнє число завдань, що знаходяться в s-му вузлі. |
 |
Середнє чіслo завдань, що знаходяться в черзі до s-му вузлу. |
 |
Середній час перебування в s-му вузлі. |
 |
Середній час очікування в s-му вузлі. |
 |
Середній час перебування в обчислювальній системі. |
 |
Середній час очікування в обчислювальній системі. |
Плановані практичні результати
Паралельний алгоритм марковських моделей багатопроцесорних обчислювальних систем дозволяють моделювати будь-які багатопроцесорні структури. Ці алгоритми можна використовувати при аналізі, синтезі й модернізації обчислювальних структур. Вони швидко обчислюються в масштабі реального часу і тому можуть використовуватися для реконфігурації обчислювальних систем в режимі реального часу.
Висновок
У роботі дано рішення актуальної наукової задачі, пов'язаної з розвитком методів і дослідження паралельного алгоритму побудови марковських моделей багатопроцесорних обчислювальних систем у корпоративних комп'ютерних мережах для аналізу якості їх функціонування, прогнозування властивостей та моделювання.
Використання паралельного алгоритму дозволяє підвищити ефективність досліджуваної обчислювальної структури.
Передбачається дослідження ефективності паралельного алгоритму побудови марковській моделі на паралельних структурах різної топології з метою з'ясування оптимальності паралельної обчислювальної структури.
Зауваження! При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2010 Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Література
1. Основы вычислительных систем. Курс лекций. Модели и методы. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://256bit.ru/education/infor2/lecture7-2.htm
2. Михайлова Т.В. Параллельный алгоритм построения дискретной модели Маркова // Искусственный интеллект. Интеллектуаьные и многопроцесорные системы. Материалы Международной научно-технической конференции, 25-30 сентября 2006г., Таганрог-Донецк-Минск, 2006. – С. 275–279
3. Мищук Ю.К. Моделирование параллельной реализации марковских моделей в многопроцессорных вычислительных системах // Наукові праці Донецького національного технічного університету. — Донецьк, ДонНТУ, 2010. – с. 238-240
4. Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. - С.17-20
5. Ефимов С.С. Обзор методов распараллеливания алгоритмов решения некоторых задач вычислительной дискретной математики. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://cmm.univer.omsk.su/sbornik/jrn17/efimov.pdf
6. Image Processing. Классификация параллельных вычислительных систем. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://iproc.ru/parallel-programming/lection-2/
7. Информационно-аналитический портал. Высокопроизводительные вычисления на WINDOWS-кластерах. Классификация вычислительных систем. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.winhpc.ru/?id=36
8. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя. — К.: ДиаСофт, 1998. — 432 с.
9. Фельдман Л.П., Михайлова Т.В. ВЕРОЯТНОСТНЫЕ МОДЕЛИ АНАЛИЗА ОЦЕНКИ ЭФФЕКТИВНОСТИ КЛАСТЕРНЫХ СИСТЕМ // Материалы второго Международного научно-практического семинара: Высокопрозводительные параллельные вычисления накластерных системах,Нижегородский государственный университет им. Н.И. Лобачевского, 2002. C. 307-314
10. Фельдман Л.П., Михайлова Т.В. Использование аналитических методов для оценки эффективности многопроцессорных вычислительных систем. //Электронное моделирование, Т.29, №2, 2007. - С.17-27
